As I’m now working as an intern in a Chinese EDA company, and also I’m doing some researches about the resource sharing problem, I found that the method used to solve this problem is simple and old fashioned. The most cited paper I found on the Google Scholar could trace back to 1990s. So I’m wondering if we can use newest method to solve this kind of problem.
Before we do so, we should first come up with an idea to express our problems so that we can use mathematic tools to solve them.
Resource Sharing Problem
read more
A Mathematic Model of Resource Sharing Problem in EDA
As I’m now working as an intern in a Chinese EDA company, and also I’m doing some researches about the resource sharing problem, I found that the method used to solve this problem is simple and old fashioned. The most cited paper I found on the Google Scholar could trace back to 1990s. So I’m wondering if we can use newest method to solve this kind of problem.
Before we do so, we should first come up with an idea to express our problems so that we can use mathematic tools to solve them.
Resource Sharing Problem
branch1:
o = a + b;
branch2:
o = a + c;
This is a simple example. As we can see, each branch has the same output o, and the equation both have two inputs and the same operator - plus. Naturally, we’ll think the actual implementation of the circuit could be two adders and one mux. Just like this:

But the fact is, most of times the compiler will convert this implementation into one mux and one adder:
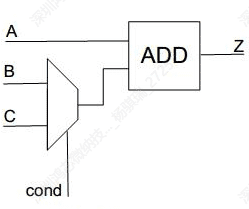
Apparently, the functions of those two circuits are the same, but the optimized one has smaller area, which means we can spend less materials two actually build this circuit.
That’s nice! But how can we know if this circuit can be shared. Also, how can we choose the best way to share since for some circuits there can be many ways to share. Take the former code as an example, we can also choose not to do the common expression elimination (in this case, is extracting the same input a), and the circuit can become two mux and one adder, whose area is a little larger than the best one.
So this is what resource sharing do - to reuse the function units to minimize the are of circuits. As you can see, this problem looks like the famous TSP problem, we need to find out the best combination to minimize the circuit’s area. However, we can’t tell if a combination is the best unless we try every possible combinations. This make this problem a little bit hard, and impossible to enumerate when the scale of this problem is too large since the complexity of this problem can be factorial, which means it’s a NP problem.
Luckily, we still got a lot of problem to do our best to approach best solution. The most popular used algorithm is the greedy algorithm, but the fatal disadvantage of it is that it can easily stuck in the local best solution. After few weeks of work, I find MCTS (aka UCT) could be probably used to solve this problem. I’ll introduce this algorithm in another blog, before that, we should use an abstract and mathematic way to express our problem to make this problem can be easily understood by the computer.
Matrix
we could take a look at a more common example.
if state == 0 begin
o = a + b - c * d;
end
else if state == 1 begin
o = b + c - a * d;
end
else begin
o = c + d - a * b;
end
first we can share multiply (or divide) operation first. These are the biggest units in actual circuit, so we should share them first. We share them by using the same method in my another blog called A Resource Sharing Algorithm Based on MCTS.
If we assign the result of multiply (or divide) to register tmp, then it can be:
if state == 0 begin
o = a + b - tmp;
end
else if state == 1 begin
o = b + c - tmp;
end
else begin
o = c + d - tmp;
end
Therefore, only plus and minus operator exists in such circuit. Then we can add bracket to the code, it should be:
if state == 0 begin
o = (a + b) - (tmp);
end
else if state == 1 begin
o = (b + c) - (tmp);
end
else begin
o = (c + d) - (tmp);
end
So we can consider the formula between two abut brackets (left and right bracket) as an ensemble, and share each part independently. Take the former part as an example, we can draw the following table:
| a | b | c | d | tmp | |
|---|---|---|---|---|---|
| state == 0 | 1 | 1 | 0 | 0 | 0 |
| state == 1 | 0 | 1 | 1 | 0 | 0 |
| else | 0 | 0 | 1 | 1 | 0 |
Then we can change this table into a matrix. Because none of those branches has the tmp input in the first part, we can ignore this input:
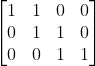
For each row, 1 means this branch has those inputs. For example, first row vector is [1 1 0 0], it means the formula of the first branch is a plus b.
Meanwhile, we can take a look at column vectors. For example, first column vector is [1 0 0], it means the input a exists in the first branch, but missed in the second and the third branch.
Let’s review our target: to minimize the area. So we can rewrite this code to:
branch1(state == 0):
tmp1 = ?
tmp2 = ?
branch2(state == 1):
tmp1 = ?
tmp2 = ?
branch3(else):
tmp1 = ?
tmp2 = ?
part1 = tmp1 + tmp2
That’s great! this circuit consists of one adder and two mux (to choose value tmp1 and tmp2 bring). So the problem is to assign value to those two registers.
You may ask: Why the assignment will influence the area? What’s the difference? Take a look of the following two cases:
Case1:
branch1(state == 0):
tmp1 = a
tmp2 = b
branch2(state == 1):
tmp1 = b
tmp2 = c
branch3(else):
tmp1 = c
tmp2 = d
part1 = tmp1 + tmp2
Case2:
branch1(state == 0):
tmp1 = a
tmp2 = b
branch2(state == 1):
tmp1 = b
tmp2 = c
branch3(else):
tmp1 = d
tmp2 = c
part1 = tmp1 + tmp2
Although both cases use two mux and one adder, but the later one consists of two 2 input mux, the former one consists of two 3 input mux to choose tmp1 and tmp2’s values. Therefore, the later one has a smaller area.
That’s done. If we use the matrix to express this process,case one can be:
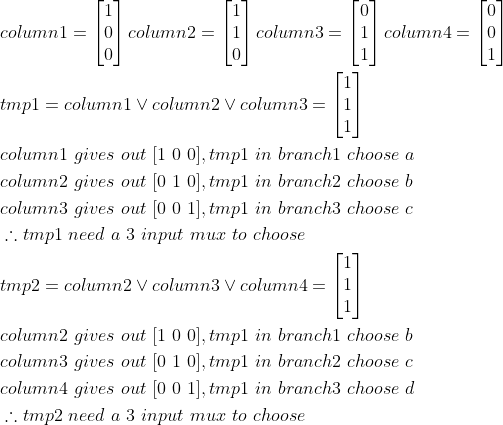
So for another case is the same, , only use two 2 input mux. Our problem become:
, only use two 2 input mux. Our problem become:
Give a matrix A with m rows and n columns, each row contains c ones and n - c zeros. Choose as little as possible columns to combine a vector which all of its elements are 1(which means it cover all branch,we call this vector as ‘one vector’).
And if we look at the choosing process, we’ll find it actually do two things: 1. All columns do or operation, if the result is not zero vector, insert the result into matrix 2. All columns do and operation, if the result is not one vector.
Take the case 1 as an example.Column1 or column2 or column3 equal to [1 1 1], and column1 and column2 and column3 = [1 1 0], so the result should be insert into the matrix, and delete the column1 and column2 and column3. And the new column or column4 equal to [1 1 1], and their and result is [0 0 0], so the process ends.
In fact, when we do or operation, we actually are working on ‘cover all branches’, but the problem is, we lose the information about the input every branch choose. So the or operation helps us to get those information.
Conclusion
So according to the content I’ve elaborated so far, we have successfully convert the resource sharing problem into a more familiar mathematic model. The next step is: How to solve?
